Без долгих слов, присущих многим книгам не только по этому направлению, вкратце объясню о чём эта книга.
Нет, вы не ошиблись. Эта книга действительно о трёхмерной графике. Но здесь здесь не будут обсуждаться такие API как Direct3D или OpenGL. Прочтение этой книги позволит вам написать собственный трёхмерный движок (или игру) со сложным текстурированием, мип-маппингом, z или даже 1/z буферизацией, прозрачностью и многими другими эффектами с нуля, то есть пользуясь только побайтовым вводом-выводом в линейный буфер экрана.
Мы будем использовать библиотеку DirectDraw для работы с экраном. Я написал набор классов для работы с этой библиотекой, что значительно облегчит нам жизнь позволяя сосредоточиться на трёхмерной графике не отвлекаясь на мелочи типа работы с экраном.
Для того, чтобы свободно читать эту книгу, вам необходимо владеть языком C++ в объёме, достаточном для того, чтобы создать класс АТД со множеством перегруженных функций и операторов, потому что более сложными вещами мы заниматься не будем. Также необходимо базовое владение WinAPI, достаточное для создания пустого окна. Желательно знание или хотя бы представление о работе экрана компьютера и устройстве видеокарты. Хотя вот всё, что вам необходимо знать в данной области: видеопамять линейна, то есть находится в памяти пиксель за пикселем, строка за строкой, слева направо, сверху вниз; а двойная буферизация - это когда мы рисуем что-то на какой-то невидимой поверхности, а потом быстро переключаем видимую и невидимую поверхности: этим достигается плавность анимации и практическое отсутствие моргания, так как видеокарта умеет делать это переключение достаточно быстро. Также хорошо было бы, если бы вы знали или хотя бы имели представление о том, что такое векторы и матрицы, и зачем они нужны в компьютерной графике: это позволило бы вам не сидеть месяцами над первой главой этой книги пытаясь разобрать, что к чему. Если вам это интересно узнать это не от меня, то я отсылаю вас к книге Андрэ Ламота "Программирование игр для Windows. Советы профессионала" (только не покупайте её в Озоне, если вы не хотите платить 2136 р. за то, что можно было бы купить рублей за 400-500 в скажем Доме Технической Книги (она там есть почти всегда).
И конечно, вы должны знать алгебру и геометрию хотя бы в объёме средней школы, потому что я не собираюсь излагать здесь основы тригонометрии и прочие темы, так как это уже сделали за меня многочисленнейшие авторы учебников по алгебре и геометрии.
Ой, слова получились долгими :)...
Двухмерные системы координат
Двухмерные декартовы координаты
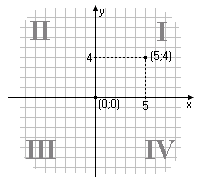
Наиболее распространённая система координат - декартова (cartesian). Декартовы координаты основаны на двух взаимно перпендикулярных осях, называемых X (ось абсцисс) и Y (ось ординат). Ось X обычно направлена горизонтально и смотрит вправо, а Y - вертикально вверх. Точки в этой системе задаются двумя параметрами: x и y. Чтобы отметить точку (x,y) на чертеже, отложите на оси X расстояние x вправо (или влево если x отрицательно), а на оси Y - y. проведите через точку x прямую, параллельную оси Y, а через y - параллельную X:
|
| Рис. 1.1. Двухмерные декартовы координаты |
|
| ||
| Квадрант | Знак x | Знак y |
|
| ||
| I | + | + |
| II | - | + |
| III | - | - |
| IV | + | - |
|
| ||
Двухмерные полярные координаты
Следующий вид двухмерных координат - полярные.
Для указания точки в полярных координатах указывают угол и длину:
Угол
|
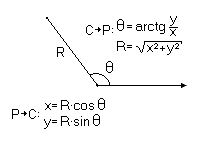
| Рис 1.2. Двухмерные полярные координаты |
Трёхмерные системы координат
Трёхмерные декартовы координаты
В трёхмерном пространстве, как и в двухмерном, самой удобной системой координат является декартова. Работает она также, как и её двухмерный аналог, только добавляется третья ось - z. Существуют и распространены две разновидности этой системы координат: левосторонняя и правосторонняя. В обоих оси x и y направлены вправо и вверх соответственно, а ось z в левосторонней направлена от наблюдателя (в экран), а в правосторонней - на наблюдателя ("торчит из экрана").
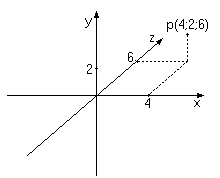
На рисунке 1.3 изображена левосторонняя система координат, ей мы и будем пользоваться в этой книге.
|
| Рис 1.3. Трёхмерные декартовы координаты |
Трёхмерные цилиндрические координаты
Если декартова система координат так просто обобщается для трёхмерного случая, то почему бы не сделать тоже самое и с полярными координатами? Но тут возникают некоторые вопросы. Сейчас "живут и развиваются" два варианта трёхмерных полярных координат: цилиндрические и сферические.
Трёхмерные цилиндрические координаты - это обычные двухмерные полярные координаты, к которым добавили ось, направленную вверх, как в декартовой системе координат. Пример трёхмерных цилиндрических координат и формулы перевода в декартовы и обратно изображены на рисунке 1.4.
|
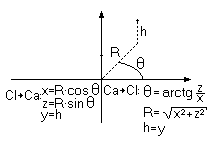
| Рис 1.4. Трёхмерные цилиндрические координаты |
Трёхмерные сферические координаты
Как уже говорилось, сферические координаты - это ещё одна разновидность трёхмерных полярных координат.
В них, вместо того чтобы добавлять ещё одну ось - расстояние - как это было сделано в трёхмерных цилиндрических координатах, добавили ещё один угол, определяющий степень отклонения точки от горизонтальной плоскости. Пример трёхмерных сферических координат и формулы перевода в декартовы и обратно изображены на рисунке 1.5.
|
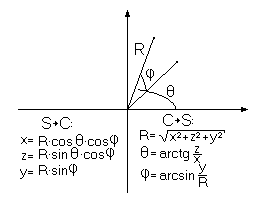
| Рис 1.5. Трёхмерные цилиндрические координаты |
Вектора
Вектора - основное понятие в современной компьютерной графике, и программист трёхмерных игр просто обязан уметь работать с ними. Вектор в математике - набор чисел. В программировании вектор используется в разных целях, но в основном - для работы с координатами. В двухмерной графике вектор определяется двумя числами, пишется как
|
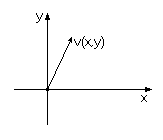
| Рис 1.6. Вектор |
С векторами можно проделывать множество разных операций, этим мы сейчас и займёмся :).
Длина вектора
Первое, что приходит в голову - найти длину той самой стрелки, которую мы только что рисовали. Это сделать достаточно просто. По теореме Пифагора сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы, этим мы и воспользуемся. На рисунке 1.7 изображены функции длины двухмерного вектора v и трёхмерного u. Длина обозначается двумя вертикальными чёрточками вокруг обозначения вектора.
|
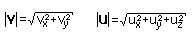
| Рис 1.7. Длина вектора |
float length ()Замечание: вычисление длины вектора требует извлечения квадратного корня, а эта операция занимает много времени, поэтому где возможно старайтесь использовать квадрат длины, который вычисляется как
{
return sqrt ( v.x * v.x + v.y * v.y + v.z * v.z );
}
x*x+y*y+z*z. Например для сравнения длин двух векторов вместо того чтобы писать u.length () < v.length () напишите u.lengthSq() < v.lengthSq (). Если длина вектора равна единице, то такой вектор называется единичным. Обратите внимание, что и квадрат длины такого вектора равен единице.
Умножение на скаляр
Следующей операцией с векторами будет умножение и деление на скалярную величину (вещественное число). Умножая (деля) вектор на скаляр его направление не меняется, а длина умножается (делится) на эту величину. В частности умножение на -1 приводит к "переворачиванию" вектора.
|
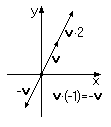
| Рис 1.8. Умножение на скаляр |
void operator *= ( float f )Деление вектора на его длину называется нормализацией и выдает в качестве результата единичный вектор того же направления, что и исходный:
{
x *= f;
y *= f;
z *= f;
}
void operator /= ( float f )
{
x /= f;
y /= f;
z /= f;
}
void normalize ()*** В этой книге нормальный вектор, соответствующий данному, будет обозначаться как v
{
(*this) /= length ();
}
Сложение векторов
Ещё одной простой операцией с векторами является сложение ( вычитание ) векторов. Складывая два вектора, мы прикладываем начало второго к концу первого и проводим новый вектор из начала координат в конец этого перенесённого вектора. Их x- и y-координаты при этом складываются. Сложение вектора с самим собой n раз аналогично умножению на n. Вычитание векторов есть сложение с обратным вектором: v-u = v+(-u).
|
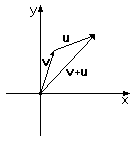
| Рис 1.9. Сложение векторов |
void operator += ( Vector3D v )
{
x += v.x;
y += v.y;
z += v.z;
}
void operator -= ( Vector3D v )
{
x -= v.x;
y -= v.y;
z -= v.z;
}
Нуль-вектор
Вы вряд ли часто будете встречать его, но он существует. Нуль-вектор это вектор, все компоненты которого равны нулю, он как бы представляет собой точку в начале координат. Сложение его с каким-нибудь вектором ничего не изменит, а сложение любого вектора с обратным даст нуль-вектор: v+0 = v; v-v = 0.
Умножение векторов
Существует несколько видов умножения векторов, самый простой из них - покомпонентное умножение, обозначаемое u
- Угол между векторами равен арккосинусу их скалярного произведения делённому на произведение их длин.
- Если скалярное произведение двух векторов равно нулю, то они взаимно-перпендикулярны.
- Если скалярное произведение двух векторов больше ноля, то угол между ними острый.
- Если скалярное произведение двух векторов меньше ноля, то угол между ними тупой.
- Скалярное произведение вектора с самим собой равно квадрату его длины.
float operator & ( Vector3D u, Vector3D v )
{
return u.x * v.x + u.y * v.y + u.z * v.z;
}
Проекции
Проекцией вектора v на вектор u называется вектор, "упирающийся" своим концом в перпендикуляр, опущенный уз конца вектора v на u:
|
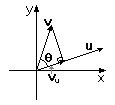
| Рис 1.10. Проекция |
Тогда
vu = u
|
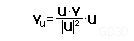
| Рис 1.11. Формула проекции |
Векторное произведение
Последним из рассматриваемых нами типов умножения будет векторное умножение. Мы будем рассматривать только его трёхмерный вариант, который будем обозначать u
u
Где
Возникает сразу два вопроса. Во-первых, таких векторов два: один направлен вверх, а другой - вниз (или ещё куда-нибудь). Ответ зависит от системы координат и порядка. В нашей с вами левосторонней системе координат если вектора передаются по часовой стрелке, то их векторное произведение направлено вверх; а если против часовой стрелки - то вниз:
|
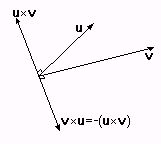
| Рис 1.12. Векторное произведение |
u
Vector3D operator ^ ( Vector3D u, Vector3D v )
{
return Vector3D ( u.y * v.z - u.z * v.y,
u.z * v.x - u.x * v.z,
u.x * v.y - u.y * v.x );
}
На практике векторное умножение применяется в первую очередь для того, чтобы получить вектор, перпендикулярный двум данным.
Радиус-вектор
Теперь расскажу для чего вектора могут применяться в машинной графике. Основное их применение - в качестве радиус-вектора. Такой вектор не рисуется как стрелка, а представляет собой одну точку (сами догадайтесь какую :)). Получается, мы всё это изучали ради каких-то точек? - спросите вы. Да, и сейчас мы научимся применять только что полученные знания в реальных целях.
*** В файлах gamemath.h/.cpp вы найдёте определения классов Vactor2D, Vector3D, Vector4D со всевозможными функциями работы с векторами. Обратите внимание что операция * - почленное умножение, & - скалярное, ^ - векторное.
Преобразования координат в 2D
Преобразования координат - это собственно то, из чего состоит большая (неважно где ударение) часть трёхмерных игр и графики. Начнём наш обзор с двухмерных преобразований, так как они в общем случае проще трёхмерных.
Перенос
Самое простое, что можно сделать с точкой - перенести её. Пусть мы хотим перенести все точки на определённый вектор (да, вектора используются и в таком виде, как невидимые стрелки из одной точки в другую, при этом его компоненты равны разности соответствующих компонент конечной и начальной точек - именно в этом порядке). Что нам необходимо для этого сделать? Взгляните на рисунок, и ответ станет очевиден: прибавить ко всем точкам вектор переноса v:
|
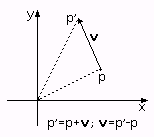
| Рис 1.13. Перенос |
Масштабирование
Масштабирование полезно, если вы хотите увеличить данный объект в s раз. При этом каждая его точка удалится от центра координат ровно в s раз, это достигается умножением всех векторов на s:
|
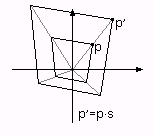
| Рис 1.14. Масштабирование |
Поворот
Поворот - самое сложное из всех перечисленных преобразований. Повороту соответствует ортонормированная матрица. Что это значит, мы поймём позже, а сейчас для нас это означает, что при повороте cохраняются длины отрезков и углы между ними.
|
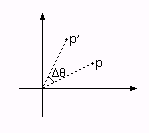
| Рис 1.15. Поворот |
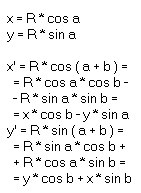Как видите, мы сначала перешли в полярную систему координат, повернули вектор в ней, а затем вернули его обратно. a - угол между вектором и осью x, b - угол поворота.Преобразования координат в 3D
Преобразования координат в 3D очень похожи на их двухмерные аналоги, только с одним "лишним" измерением - осью z.
Перенос
Перенос в 3D полностью аналогичен переносу в двухмерном случае: к точкам просто прибавляется вектор переноса.
Масштабирование
Масштабирование опять же полностью аналогично двухмерному: точки умножаются на коэффициент масштабирования.
Поворот
С поворотом дела обстоят несколько сложней. Повороты в трёхмерном пространстве бывают трёх видов: вокруг оси x, y или z. Все они абсолютно аналогичны двухмерному повороту. Более подробно мы рассмотрим повороты когда мы будем проходить матрицы.
Матрицы
Вот мы и подошли к главной теме этой главы.
Матрицы в трёхмерной компьютерной графике используются как главный инструмент преобразований. Они позволяют выразить все изученные нами преобразования а также многие другие в единой форме. Также мы можем применять эти преобразования, находить к ним обратные и объединять несколько преобразований в одно. Но сначала нам надо узнать что они из себя представляют и как с ними работать.
Добро пожаловать в Матрицу :)
Матрица - прямоугольная таблица чисел (или чего либо другого). Можно также рассматривать матрицу как "вектор векторов", но этого мы с вами делать не будем. Матрица имеет свою размерность - размер этого самого прямоугольника. Если размерность матрицы m на n, то в прямоугольнике m строк и n столбцов. На рисунке изображены матрицы A2
|
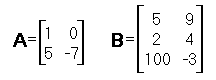
| Рис 1.16. Матрицы |
С матрицами, как и с векторами можно производить множество операций. *** Существует два основных вида матриц: row-major column-major. Не буду особо объяснять разницу, скажу только, что мы будем использовать первую.
Сложение матриц
Сложение и вычитание матриц выполняется почленно, как и с векторами. Складываться (вычитаться) могут только матрицы одного размера, а результатом является матрица того же размера. Не буду показывать пример, поскольку он займёт много места :).
Умножение на скаляр
Ещё одна почленная операция, не буду объяснять подробнее.
Транспозиция
Транспозиция - это как бы "переворачивание" матрицы. При транспозиции элемент Mi,j (i-тая строка, j-тый столбец) меняется местами с Mj,i. При этом размеры матрицы тоже меняются местами: ширина становится высотой, а высота - шириной.
*** В нашем обозначении левый верхний элемент матрицы имеет индекс 0,0, а не 1,1, как в математике. Это объясняется тем, что в C++ индексация массивов начинается с нуля, а матрицу мы будем хранить как массив.
Умножение матриц
Вот мы и подошли к главной матричной операции. Во-первых, матрицы умножать можно только если количество столбцом в первой равно количеству строк во второй. То есть умножать можно только матрицы вида [m
Так по какому же правилу вычисляются элементы результирующей матрицы?
Элемент с индексами i,j будет равен скалярному произведению i-той строки первой матрицы на j-тый столбец второй матрицы (под скалярным произведением строки и столбца подразумевается произведение векторов, состоящих из тех же элементов):
|
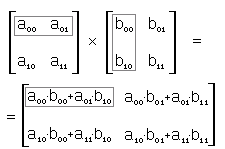
| Рис 1.17. Умножение матриц |
Единичная матрица
Единичной матрицей называется квадратная матрица, все элементы которой равны нулю кроме тех, которые стоят на главной диагонали (сверху вниз, слева направо), которые равны единице:
|
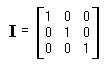
| Рис 1.18. Единичная матрица |
Преобразования и Матрицы
Вот теперь, когда мы познакомились с матрицами и основными операциями над ними, мы можем начать делать то, зачем написана эта книга. Естественно, только после того когда мы поймём, зачем нам эти загадочные математические объекты.
Умножение матрицы на вектор
Как вы могли заметить, вектор - тоже своеобразная матрица (ну чем не матрица? прямоугольник, только высотой 1). А, значит, и умножать его можно на матрицы. Вот, например, умножив трёхмерный вектор на матрицу 3
Однородные координаты
Для "удобства" обращения и для расширения круга воздействий, оказываемых матрицей на вектор, были введены так называемые однородные координаты. То есть взяли трёхмерный вектор и добавили четвёртое число, w. Получили четырёхмерный вектор. Но зачем? Так я уже сказал: для расширения набора возможных действий, оказываемых матрицей на вектор. Обычно четвёртая координата, w, равна единице. А если в результате преобразования она изменится, то мы на неё поделим весь вектор. Чтобы понимать, чего мы этим добиваемся, попробуйте потренироваться в умножении вектора на матрицу (кстати умножать матрицу на вектор не получится. Почему?). Очень скоро вы заметите, что в первом столбце описано, как x зависит од других координат. Он равен
a00*x + a10*y + a20*z [+ a30*w]. Аналогично для y, z и w. Это нам и надо, сейчас мы этим и воспользуемся.
Матричные преобразования
В этой и последующих секциях будут приведены примеры матричных преобразований. Я опустил преобразования в 2D.
Матрица переноса
Матрица переноса выглядит как единичная матрица 4x4, только её последняя строка равна вектору переноса (в однородных координатах):
|
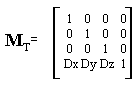
| Рис 1.19. Матрица переноса |
А это как раз то, что нам требовалось.
Матрица масштабирования
Матрица масштабирования выглядит как единичная матрица 4x4, только первые три единицы заменены на коэффициент s:
|
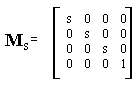
| Рис 1.20. Матрица масштабирования |
Матрица поворота
Матрица поворота описывается по формуле, выведенной нами ранее (их три):
|
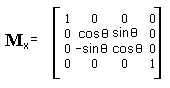
| Рис 1.21. Поворот вокруг оси X |
|
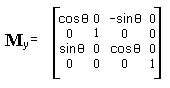
| Рис 1.22. Поворот вокруг оси Y |
|
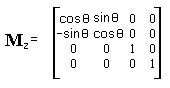
| Рис 1.23. Поворот вокруг оси Z |
Применение матриц
И несколько слов о применении матриц в реальной жизни.
Если мы хотим подвергнуть вектор v преобразованиям X и Y, то мы сделаем следующее:
pnew = p * X * Y;
Но если таких точек миллион, а матриц всего две? Тут происходит такая хитрость: сначала перемножаются между собой X и Y, а затем все вектора умножаются на результат:
Matrix4D mul = X * Y;
for ( int i = 0; i < nVerts; i++ )
vert [i] *= mul;
Это сработает потому что, как я уже говорил, ( p * X ) * Y = p * ( X * Y ). Этот полезный трюк очень активно применяется в программах.И ещё. Конечно, матрицы = это круто, но не переусердствуйте: бессмысленно использовать матрицу просто для переноса: 3 сложения (без матриц) или 16 умножений и 12 сложений (с матрицами). Вообще избегайте умножения на разреженные матрицы (где много нулей и единиц).
Резюме
В этой главе мы повторили двухмерные и трёхмерные системы координат, изучили вектора и основные операции над ними, основные двух- и трёх- мерные преобразования, матрицы, операции над матрицами, преобразования, выполняемые с помощью матриц.
Классы Vector2D, Vector3D, Vector4D, Matrix4D и некоторые константы вы найдёте в файлах gamemath.h/.cpp, которые входят в состав GameLib (обновлено 28 июня, исправлены баги в этой библиотеке). Потратьте время на их изучение, потому что следующая глава, возможно, будет ещё не скоро.
Наверх
Содержание
GameLib
Написано 6.28.05 ReaVeR'ом для GameDev3D.
Текст свободно распространяется при условии неизменности содержимого и этой подписи.
Мой e-mail: adkolosov@programmer.net
